哈勃常数 (Hubble Constant) 是描述宇宙膨胀速率的重要参数,作为宇宙学模型的核心参数,哈勃常数对于天文学有着举足轻重的研究意义,而哈勃常数的测定一直以来也是天体物理学中的重要研究领域。常见的测量方法,一种是通过标准烛光法测量星系的距离,以及谱线位移求出的星系退行速度,再通过哈勃定律可求得哈勃常数。一种是基于宇宙学标准模型,通过对于宇宙微波背景辐射 (CMB) 的观测,计算取得数值。而在方法一中,测量距离通常通过测量选定的“烛光”的视星等,结合其已确定的绝对星等,通过视星等与绝对星等的关系式确定距离,或者基于周期光度关系对于特定的脉动变星观测测定距离。本课题旨在初步比较探究几种典型以及最新提出的测定方法,尤其以标准烛光法及其衍生方法为主,通过结合相关数据以及对于方法本身的原理进行分析,从而横向比较这几种常见的测量哈勃常数的方法,并由此对哈勃常数的多模态测算进行初步探究。
关键词:哈勃常数 标准烛光法 脉动变星 Ia型超新星 造父变星

一、 引言 1
(一)课题背景及介绍 1
(二)课题研究内容简介 2
1.2.1 哈勃常数测定方法原理概述 2
1.2.2 基于标准烛光法及其衍生方法介绍 2
1.2.3 其他方法简介 4
(三)网上查新情况 5
(四)数据介绍 6
二、 测量方法比较分析 6
(一) 基于Ia型超新星方法测量比较分析 6
(二) 造父变星法及其他方法测量结果分析 10
2.2.1 造父变星法测量哈勃常数详细分析 10
2.2.2 其他方法分析(以TRGB法为典型) 11
(三) 各种测定哈勃常数的方法的比较分析及总结 12
三、 哈勃常数的多模态测算以及其物理意义初探 12
(一) 不同测量方法比较和互补性 12
(二) 各种测量哈勃常数方法的研究测量结果分析 13
(三) 各种测量哈勃常数方法的结合应用及哈勃常数测量的物理意义初探 14
四、 结论及展望 15
(一) 综合性总结 15
(二) 不足与相关展望 15
五、 参考文献 16
哈勃常数(Hubble Constant)是描述宇宙膨胀速率的重要参数,作为宇宙学模型的核心参数,哈勃常数对于天文学有着举足轻重的研究意义,通过哈勃常数对于宇宙年龄,宇宙模型的建立验证以及宇宙膨胀等诸多领域有着重要价值。
哈勃常数的测定一直以来是天体物理学中的一个重要研究领域。一百年前,哈勃提出了著名的“哈勃关系”,由于当时的天文观测技术有限,早期的哈勃常数测定有很大的不确定性,随着各种技术发展,哈勃常数的测定逐渐精确,截止到2015年,目前主要采用的哈勃常数数值为 67.74 ± 0.46 km/s/Mpc (由ESA的普朗克探测卫星测定)。
由于各种观测技术的提升,各种测定哈勃常数的方法不断被提出与研究。一百年来,人们一开始基于天体的理论光度和测量光度的关系求取天体距离,测量哈勃常数,典型方法为将Ia型超新星作为标准烛光测量到其宿主星系的距离,来求取哈勃常数,或者基于造父变星的周光关系来测距,同理测得哈勃常数;而如今人们已经形成了多方位多信使测量哈勃常数方法,通过引力波,或者基于宇宙微波背景辐射的声学震荡等方法,结合更为先进的光学测距,来得到更为精确的哈勃常数。
基于此,本课题初步比较探究几种以基于光学关系为主的哈勃常数测算方法,其中包含几种最新的测算哈勃常数方法,并通过结合相关数据及各方法原理,进行分析,从而横向比较这几种测量哈勃常数的方法,为哈勃常数的测定提供了多元视角和途径选择上的参考。
1.2.1 哈勃常数测定方法原理概述
根据 Hubble-Lemaître (Hubble) 定律,可由星系视向速度(退行速度)推算星系距离,而通过视向速度与星系距离也可测算𝐻0(哈勃常数),如下1.1式
𝑣 = 𝐻0𝑑 (1.1)
由于通过按照上式,越是遥远的星系,退行速度越大,当速度大到一定程度时,需根据狭义相对论推导出的严格 Doppler 公式计算速度,如下1.2式
(1.2)
由此公式可知,要测定视向速度,可由测定星系的红移量z计算得到。对于红移量z的测定,当今主要采用对于星系的普遍红移进行测量。而对于距离d的测定,根据不同的天文原理,则可以产生不同的测量手段与方法[1][2]。
1.2.2 基于标准烛光法及其衍生方法介绍
基于上文对于距离的测量手段不同可以产生不同的测量方法,当今对于不同天体的光学性质,提出了多种光学测距方法。我们知道一个光源发出的光,其亮度和与观测点的距离的平方成反比, 这些方法大多数是将一类天体可以根据理论预测其光度,并通过实测光度,根据光度与距离的关系,从而测得距离,再通过对于天体所在宿主星系的红移量观测,求取哈勃常数。
而这种选取的有着规则性变化或稳定性光度的天体被人们称为宇宙中的标准烛光。
本课题主要探究的基于以上光学原理方法有如下:
第一种,Ia型超新星作为标准烛光测量。
作为早期也是经典的测量方法,Ia型超新星一直以来扮演着重要的测量工具。由于其明亮,峰值光度稳定,Ia型超新星常被用作标准烛光的测距手段。
Ia型超新星本身由双星机制产生,也就是从红巨星伴星处吸积物质的一颗富碳白矮星在超过钱德拉塞卡极限后引起碳燃烧,导致超新星爆发。而Ia型超新星有个重要的特点是其在光极大的时候真亮度是趋同的,绝对星等均在-20等左右(国际主流认为在-19.3等),利用这个特点,我们结合望远镜观测到的超新星视星等,于是可以根据下式计算距离,
𝑚 = 5 𝑙𝑔 𝑑 + 𝑀 − 5 (1.3)
其中将距离模数μ定义为m-M,但由于Ia型超新星在河外星系中未有广泛观测数据,使得合适的超新星数据成了该研究方法的重要问题,再结合将电磁波作为媒介的观测方法通病(电磁波从星体发射出来易受到宇宙尘埃影响),导致该方法所得结果仍就有不少误差。[2][3]
第二种,造父变星法。
与Ia型超新星同为早期且经典的超新星测量方法,其原理是基于造父变星的周光关系,来测量距离。造父变星是一类光变周期较短(1~50天)且周期较为稳定的脉动变星,其多为黄色的巨星或超巨星,较为明亮,典型的如仙王座δ星(造父一);而该类变星的显著特点是其光变周期和其光度存在某种数量关系(周光关系),根据大量观测数据,表明造父变星主要分为两类:经典造父变星和室女座W型变星,两类变星的周光关系公式如下:
𝑀𝑃 = −1.80 − 1.74 𝑙𝑔 𝑃 (1.4)
𝑀𝑃 = −0.35 − 1.75 𝑙𝑔 𝑃 (1.5)
上式中,P为光变周期,M为绝对星等,结合1.3式,我们不难得出造父变星的距离,从而测得哈勃常数。
造父变星作为经典量天尺,其问题也不难发现,周光关系主要为根据大量数据的来的经验公式,无严格的理论推理,也造就了造父变星测算的哈勃常数误差[4]。
第三种,基于蒭藁变星测量法。
刍藁变星(Mira变星),是一种长周期脉动变星,典型星为鲸鱼座ο星(蒭藁增二),可以根据类似第二种方法测量哈勃常数,但是由于此类变星光变周期过长,往往有几十年甚至几个世纪,不利于观测,该类方法一直未能成为主流测量方法[4]。
第四种,红巨星分支技术测量。

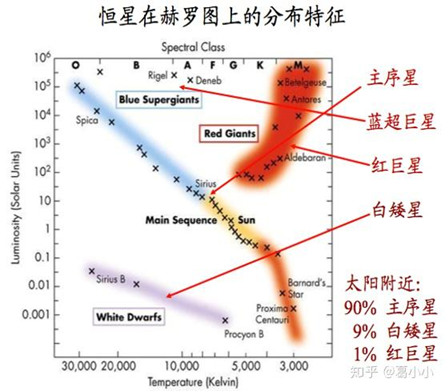
近年来,红巨星分支技术(TRGB)测量距离的方法也逐渐兴起,由芝加哥的研究组Freedman 等人提出[5],在赫罗图(H-R)(如图2)上红巨星分支的恒星,在基于经验性质的公式和其恒星学理论的结合下,形成了一个良好的标准烛光。由于恒星进入TRGB阶段时标志着低质量红巨星核心氦燃烧的开始,在此阶段,红巨星的光度具有明显不连续性,且有着明亮的红色,便于识别,再加上理论上对于该类恒星的绝对星等计算,结合视星等,便可测算距离,从而测算哈勃常数。

Freedman等人指出,该测量方法相较于传统的测量的方法,受宇宙尘埃影响较少,且观测效率高,普适性强,且易于识别,是良好的标准烛光。
第五种, 特殊波段的渐进巨星分支来帮助测量。
最近基于JWST望远镜的观测数据,新提出的位于近红外颜色星等图中的J-区域渐近巨星分支(JAGB)中的恒星,可以成为潜在的标准烛光[6]。类似于TRGB,由于其光度稳定较高,且易于识别,其观测效率较高,普适性强,并且由于JAGB主要在红外波段进行测量,其光度测量对金属丰度和消光的影响较小,使其更适合用于测量河外星系的距离。由此,该类渐进巨星分支上的恒星也可用来测量哈勃常数。
此外,根据一些其他的明亮稳定的恒星或天体,如球状星团,O,B 型超巨星等,同样可被选取为标准烛光。由于其本身的不普适性,本文也不再赘述。
1.2.3 其他方法简介
而除了相关基于光学性质,尤其以“标准烛光法”为主的测量方法外,一些其他科学原理的测量技术也逐渐兴起。
这类方法中,典型的如基于几何测距,得到星系距离的方法,例如近年由上海天文台参与的“河外水超脉泽盘”就利用了这一原理[7],该测距方法同时在测量视向速度方面也有着特殊的方法:由于在一类天体中,其中心有一个超大质量黑洞。在距离黑洞约1秒差距的吸积盘区域上,分布着大量水分子。在吸积盘区域,这样的水分子可以产生22 GHz水超脉泽辐射。通过甚长基线干涉测量 (VLBI) 技术,对脉泽斑视向速度进行精确测量。同时对于视向速度的长期观测,得出其与黑洞的物理尺寸,结合已测得的脉泽盘角尺寸,利用几何距离方法,求取距离,再求取其哈勃常数。该方法相对于已有测量哈勃常数的方法,较为独立,有助于验证与提升哈勃常数的精确性。
另一类典型的测量方法,就是近年来较为主流的基于宇宙微波背景辐射测量哈勃常数的方法。该方法通过对于宇宙微波背景辐射 (CMB) 的观测,结合宇宙学标准模型,直接计算哈勃常数。其原理为通过对于宇宙微波背景辐射中的重子声波振荡大小测量,测算宇宙微波背景辐射出现时的宇宙红移量z,通过带入宇宙学模型计算哈勃常数。上文中ESA的普朗克探测卫星就通过该方法确定目前主流采用的哈勃常数数值。
通过引力透镜结合光的偏转导致的时间差也可以测量星系距离,此外通过引力波测量星系距离,再结合红移量测量哈勃常数的方法也同样值得关注,该方法中,由于引力波不受宇宙尘埃影响,相对于光学测距,其测距更具有稳定性与精确性,被称为“标准汽笛”,并可以独立限制哈勃常数。结合光学方法,对于星系进行多信使测量,可以得到更精确的哈勃常数数值。
由于课题篇幅所限,本文还是主要针对于1.2.2中的光学方法做探究与分析。
截至2023年12月底,根据在中国知网查新情况,以“哈勃常数”“哈勃常数测定”“标准烛光法”“哈勃定律”为关键词进行搜索,结果如下,“哈勃常数”为关键词的搜索结果为373项,以“哈勃常数”测定为关键词进行检索,为8项,以“标准烛光法”为关键词搜索,结果为90项,以“哈勃定律”为关键词检索,结果为140项,其中大多数检索结果为科普期刊文章或者综合性报告,可见近年来对于哈勃常数的研究呈密集状态,而与本文哈勃常数的测定的探究分析较为相关的文章,数量并不占多数,并且多为着重对宇宙学模型的验证,对于哈勃常数本身的多模态测量文章,多数是基于一种方法为主的介绍,如2018年由华东师大的王焘的论文“通过引力波测量哈勃常数”[8],或者基于多方法做横向比较,但是多数论文并未严格分析各种方法的特征,且与本文以光学原理测量哈勃常数的方法为主进行比较分析的课题内容也并不一致,如近年的两篇以“哈勃常数危机”为题的文章[9][10]。
由于本文探究的主要方法为1.2.2中的几种光学方法(以第一种,第二种,第四种为主),在选取数据方面,本课题主要还是基于对一些论文已总结的恒星数据和测量结果方法进行综合分析。
而本课题在针对超新星的哈勃常数计算方法特别进行了相关的数据带入计算,以便更好的了解和分析相关的数据。其中针对于Ia型超新星的相关数据,主要选取了由 2018年 Scolnic 等人发布的超新星数据集 Pantheon(万神殿) ,同时参考了近年新发表的 Pantheon+ 数据[11][12]。
Scolnic等人在选取了一系列典型Ia型超新星后,整理了一组包含了1048个Ia型超新星样本。在该样本中,Ia 型超新星的距离模数µ来自于SALT2光变曲线拟合器对光变曲线的观测。而 Pantheon+ 则包含了1624个超新星数据和77个造父变星数据(1500个超新星和43个造父变星),是更为强大的数据库。基于对这些数据的基础分析,结合主流的研究方法原理分析,本文将在下文具体运用这些数据对Ia型超新星测量哈勃常数的方法做具体阐述。
通过对Ia型超新星数据库Pantheon的数据原理方法调查,我们可以得到已处理的数据红移量和其视星等,如下表(3.1),我们节选了1024个超新星数据组中的10个,作为示例样本分析,以便更直观显示后续的数据操作处理,其中 zcmb 作为宇宙学红移,zhel 作为光害红移,dz 是红移量的误差,而 mb 代表距离模数 μ 减去绝对星等,即视星等,dmb 是视星等测量产生的误差。
表3.1 Pantheon 超新星数据库(节选)
我们根据较为简单的方式对于表中数据进行初步计算,由于表中红移量大多处于0.2到0.6之间,我们采用通用的多普勒公式:
𝑣 = 𝑐𝑧 (3.1)
计算其视向速度,与通过式1.2计算所得视向速度,互相比较发现,对于1024个超新星的通用公式测量的v和严格多普勒公式测量的v存在较大误差,达到17%(基于全数据的误差计算分析),因此我们选择严格多普勒计算,得到视向速度𝑣。
其次对于 mb 的处理方法,我们将 dmb 作为误差带入,以上述数据为例带入,得到下方节选数据的红移量与视星等关系图(表3.2),该图展现了红移量与视星等关系,结合误差棒,我们可以看到z与mb基本上呈指数函数关系。
结合理论预测,根据上文式1.3的变式,可以得到以下公式(3.2):
𝑑 = 100.2(𝑚−𝑀+5) = 100.2𝜇+1 (3.2)
由公式可知,z与mb存在指数关系,意味着退行速度 v 与 m 存在线性关系。

表3.2 Pantheon 节选数据原始红移量与视星等关系图
拓展到1024个数据中,也是这样,由于数据量庞大,其图像无法精确分析,但经过指数拟合,可以得到z与mb基本呈指数关系,如表3.3
表3.3 Pantheon数据原始红移量与视星等关系图
因此,我们可以结合3.2式对数据进行处理,根据Ia型超新星绝对星等为-19.3m,结合误差带入,得到退行速度与光度距离的关系,如表3.4,v 与 d 基本成线性关系,其斜率的大小在数值上就为 H0/c,结合全数据,再次通过散点图绘制,通过线性拟合,即可获得这种线性关系的系数,转换为哈勃常数,约为29.462。不难发现,这与国际主流测算出来的 67.74 ± 0.46 km/s/Mpc 相差甚远,并且结合图像,我们可以发现,整个图像的斜率随着距离的增大,斜率逐渐出现变缓,当我们取距离小于 2000 Mpc 的数据统计,会发现其测算出的结果接近52,如表3.5,这一方面证明了直接通过Ia型超新星原始数据计算哈勃常数的不可行性,一方面也证明该方法单一运用存在误差。
表3.4 pantheon 节选数据求取的退行速度与光度距离的关系图
表3.5 pantheon 数据求取的退行速度与光度距离的关系图
结合上述测量原理分析,该误差导致原因,可能由于以下多方面,第一,视星等本身的误差,由于,较远的超新星更有可能受到星际尘埃的影响,导致其观测到的光度实际已经发生改变,产生误差;第二,由于宇宙学模型自身的原因,可能出于暗物质暗能量的分布情况也导致了这种不同距离的斜率不同情况。
针对于以上的测量误差,由于距离模数 μ 的差异,而导致哈勃常数的简并性,研究人员通过对哈勃常数的边缘化处理,通过最小化卡方函数,使得到模型与观测数据最符合的参数组合,从而得到更有精度的哈勃常数[11][13]。基于此,根据 Scolnic 研究组的最新相关计算,再结合新发布的 Pantheon+ 数据,测算出来哈勃常数为 73.4(km/s)/Mpc,不确定性仅为1.3%,这与主流认为的哈勃常数值已很接近。
2.2.1 造父变星法测量哈勃常数详细分析
造父变星作为一种经典的方法,其测量哈勃常数原理已在上文有所论述,而对于不同星族类型的造父变星,可能产生不同的测量后果,星族I的造父变星较为明亮,是理想的标准烛光,但是位于星盘内受星际消光影响严重,而星族II虽较暗,主要为老年造父变星,但是其不需像星族I型进行繁琐的消光处理。星族II可以根据其光变周期分为三类变星, 其中室女座W型变星就是典型的一类。
造父变星如上文叙述,通过周光关系来测定距离,这种周光关系(PL关系),其原理主要通过非PL关系方法测出造父变星距离,并得出经验公式,即PL关系,这种PL关系所需要的两个重要变量是其图像中的斜率和零点,而这种距离方法,主要总结为以下几种,第一,视差测量法,第二,主序拟合法,第三,综合测量法(多模态测量)。
其中,视差测量法较为传统,分为统计视差法,移动星团视差法,三角视差法。三种分支方法,第一种,是通过使用大量的星系或星团中的造父变星进行统计学上的视差测量。第二种,则利用星团中的造父变星,通过星团的几何和运动信息来测定距离。第三种则是传统的地球与天体的视差角来测量;而主序拟合法则十分巧妙的对于目标造父变星所在的星系或者星团的主序星测光和比较光度来确定距离。该方法得到的结果更为精确。现今人们往往通过不同的独立方法对于造父变星的PL关系进行多模态测量,从而得到普适性的造父变星周光关系,而更进一步,基于PL关系,人们又提出了新的经验关系即PLC关系,通过周期P,光度L和颜色C可得到更稳定与精确的造父变星关系式。
基于以上的方法,我们可以根据总结的经验公式,对于普适类型的恒星测量得到较为精确的造父变星绝对星等数值,接着根据距离模数关系式,反求出距离,接着测量哈勃常数。可以说,结合多种测量造父变星距离的方法,这些经验公式也对于距离起到反限制作用,让测量更为精确[14]。
以上的造父变星法,同时缺陷也有很多。显而易见的经验公式通病,对于造父变星的经验公式,要得到更为精确的公式结果,就需要更庞大的数据集,同时对于这个关系的不断拟合,人们也发现本身PL关系的斜率也并不是恒量,而是随着光变周期有变化,于是有人提出了非线性PL关系式。
此外,受限于造父变星本身的结构影响,造父变星本身的金属度或许也对变星的关系有所影响。
2022年期间,Reyes 和 Anderson 的两个研究小组[15]利用造父变星测得的结果为73.04 ± 1.04km/s/Mpc
2.2.2 其他方法分析(以TRGB法为典型)
其他的基于光学原理测量方法,多为今年来新提出的测量哈勃常数方法,比较典型的如 Freedman 研究组提出的TRGB法[5](上文有所基本介绍),该方法简单来说就是对于较为明亮的红巨星分支上的恒星进行测量,由于该类恒星明亮,易识别,光度稳定的特点,根据距离模数关系式便可得到其距离。
使用RGB法测量距离的例子已经十分久远,1918年就有研究人员在球状星团的色星等图中使用明亮的巨星作为烛光测量距离。
TRGB所基于的RGB红巨星分支的尖端处,作为测量标定点,由于从该点开始,低质量红巨星核心氦开始燃烧,由此其星等颜色图出现显著的不连续,使TRGB部分成为可靠的测量标定点。研究团队根据 HST 的 F814W 滤波器(基于I波段)测定相关数据,在I波段(红外波段)中,TRGB在颜色与金属丰度呈现相对平坦的光度,通过全光通校正,利用恒星模型和色指数修正,将I波段的光度转换为天体总光度测量,从而得到距离。在I波段上测量,不仅减少了星际尘埃的消光影响,同时该波段红巨星特诊明显。综合以上优点,此类方法,有助于测量结果的稳定,但缺点在于其对于特定波段的依赖性等问题上等。Freedman研究组根据该方法测得的哈勃常数数值为 69.8 ± 1.9km/s/Mpc ( H0 = 69.8 ± 0.8 (±1.1% stat) ± 1.7 (±2.4% sys) km/s/Mpc )。
与TRGB类似的JAGB,随着JWST的升空,近期被提出[6](最新的相关研究可以在arXiv的预印本存储库中查阅)。其原理则是将目光瞄准了AGB分支上的J波区段(近红外波段),对于渐近巨星分支的JAGB星体观测,类似于TRGB,得出其距离。近年来随着JWST的升空才逐渐被深入研究,将来随着JWST的海量数据库被不断发布,JAGB作为一种较为精确的标准烛光,是精确测量哈勃常数的潜力所在,2023年末,新的研究根据此方法得出了 74.7 ± 3.2km/s/Mpc (H0 = 74.7±2.2 (stat) ± 2.3 (sys))。
以上众多方法,通过归纳总结,可以主要被分为两类,一类是选取明亮的且较为稳定的天体作为标准烛光,如Ia型超新星,TRGB,JAGB一类是选取规则脉动的变星作为标准烛光,如本文详细阐述的造父变星,还有上文曾提过的刍藁变星。无论如何,这些独立于宇宙学模型之外的光学途径测量,在近年来依旧占主流测量哈勃常数方法,并为哈勃常数的测定提供多模态测量数值。
通过前文对于各种基于光学理论的测量哈勃常数方法分析,我们可以进行初步比较探究各种测量方法的局限性和精确性。
Ia型超新星,其特点在于有稳定的峰值光度,其优势在于星体较为明亮,且相关测距技术成熟,测量精确,并且随着样本数的提升,测量精度可以不断提升,是良好的标准烛光,但其局限性在于易受到各种干扰,其受到星际尘埃的影响,以及宿主星系的特诊影响较为明显,虽然如上文实验数据中,其初始测得的哈勃常数数值随着距离发生改变,但尽管受到一些误差影响,其峰值光度的稳定性也让宇宙红移对其光度影响教弱,使得高红移的星系中,Ia型超新星常被用做标准烛光。结合最终研究人员处理的实验数据,该方法的不确定性也较其他方法较低。
造父变星法,由于其光变稳定性和其普遍性,曾被广泛用于哈勃常数测定,结合其经验公式,能够得到更多具有经验意义的测量值,但其缺陷也正是由于经验性导致的缺乏理论阐述,而失去的精确性。
TRGB法,作为易于识别和观测的一类星体,其优势在于稳定性和易识别性,并且在红外波段观测,也减少了消光作用,结合其测得数据和基于CMB测得的数据,有着很强的近似性,也证明了其精确性。其缺陷在于对于恒星群体等方面有着严格的要求,并且观测高红移星体时,往往受红移影响导致观测困难。
JAGB法,作为近红外波段的观测对象,其优势在于对尘埃消光不敏感,并且随着JWST的数据发布有着良好的前景,缺陷在于其需要准确的测量数据,与TRGB类似,需要对于特定的天体进行特定的观测。
综合分析,这些方法出于自身的光学性质不同,基于同一原理,却可以进行互补。对于一些高红移星系的测量,往往采用经典的Ia型超新星和造父变星,对于低红移星系,则选取JAGB和TRGB法。而往往,在通过一种方法测量完星系的距离后,可以采用Ia型超新星或造父变星进行辅助测量验证,对哈勃常数范围进行限制。
基于以上光学方法测量的结果,通过多模态测量哈勃常数,我们可以对其代表性的研究测算结果进行平均值求取,以便更好的了解光学原理测量哈勃常数的意义。
采用普通的平均值算法,得到的四组哈勃常数结果平均值约为72.7± 1.8km/s/Mpc。
我们也可以通过误差求取每一种方法测量结果的不确定性σ,定义得到每种方法本身的确定性为(1-σ),将其作为权重对于四个数值加权平均运算求出更有精确意义的数值,72.73km/s/Mpc。
两种方法所得结果较为接近,且与CMB测得的哈勃常数也较为接近,证明了光学原理应用于哈勃常数测量的可靠性。
在以上光学原理测量的方法基础上,可以结合其他媒介的测量结果进行相互验证限制。比较典型的就如运用CMB(宇宙微波背景辐射)的重子声波振荡BAO大小测量,结合宇宙学模型公式进行计算。由于较为遥远的宇宙时空里,在宇宙大爆炸发生后,宇宙处于高密度炙热状态,光子和重子耦合在一起,当其解耦时,光子形成了当今看到的CMB,当大爆炸约38万年后,光子不再与重子作用,此时遗留下来的星系的距离逐渐固定在BAO尺度上,通过基于该原理,对于CMB和星系分布以及声学振荡的测量观测,再根据宇宙学模型,可以推出哈勃常数的大小[1]。
这种方法测量的哈勃常数时根据理论严格推理得到的模型结合较为精确的测量得到的,具有较为精确和严谨的特点,但是由于缺乏理论的完备性,且由于目前对于宇宙学的重要组成部分为尚未深入研究的暗物质和暗能量,当前根据该方法计算的常数仍有很大的未知性。
而光学原理的测量结果正对于宇宙学原理测量结果起到了限制作用,并为验证宇宙学标准模型的正确性提供数据支持。
近年来,多信使天文学的发展值得关注,对于某一天体进行多信使(多媒介)测量,以便于更好的理解天体本身。常用多信使测量方法是通过引力波和电磁波测量,基于该原理,我们将其可应用于哈勃常数测定上,对于遥远星系进行引力波和光学测量,两种相互独立方法共同得到更为精确的星系距离。
哈勃常数测量的物理意义在此也显示出来,一是作为宇宙学重要参数,其测定对于宇宙学模型建立的影响有着举足轻重的地位,二是其作为描述宇宙膨胀速率的常数,其意义对于研究宇宙演化和生命历程也有着重要价值。此外,哈勃常数的测定一方面依赖于测距方法的提升,一方面也反作用于提升各种测距方式。
本课题总结并介绍了一系列的基于光学原理的哈勃常数测量方法,并主要从原理结合数据分析了四种较为有代表性的测量方法,其中两种是最新提出的测两方法。并最终基于原理分析,横向比较和分析了各种方法的优势与局限和互补性,基于此而进行初步多模态分析哈勃常数,验证了光学原理测量哈勃常数的可靠性和优势。
总之,本课题通过基于几种哈勃常数测量方法的对比和初步探究,提供了多个测量哈勃常数的视角,并系统性总结分析了光学原理下的哈勃常数测量技术,对于基于光学原理的哈勃常数测算方式选择,有着有益的科学意义和参考,通过本课题,也有助于加深对于哈勃常数多模态测量的理解和认知。
由于本文作者能力有限,在对于哈勃常数方法的分析之余,对于哈勃常数的测定的数据处理能力还有待提升。但是通过本课题,也加深了本文作者对于哈勃常数测定方法的学习与理解。
同时,在未来,本课题将继续朝着以下方面展开,第一,获取更多的天文数据。结合近年来中国国家天文台的LAMOST巡天数据集,尤其是近期发布的dr11数据,和近期公开的dr9数据,以及近年来JWST对于深空的红外波段研究数据,近年来LIGO引力波观测台的引力波数据,基于更多的测算方式,从数据源头上选择,来促进对哈勃常数测算的研究。
第二,结合近年来多信使天文学的不断发展,对于单一天体的多种独立方法测量,从多模态多方法运用的原理来研究更为精确的哈勃常数数值。
第三,同时结合最新的研究方式,如上文提到的JAGB法和对河外水超脉泽盘的测定,来从方法本身上寻找更为精确的哈勃常数测量方法。
以上为对于本课题的不足与未来的展望,结合本课题提供的几种测量哈勃常数的方法,相信随着技术的不断提升,哈勃常数的测定也将越来越精确。
[1]天体物理学[M].,:500.
[2]天文学新概论 第4版[M].,:464.
[3]基础天文学[M].,:402.
[4]天体物理概论 彩色版[M].,:333.
[5] Wendy L. Freedman , Barry F. Madore , Dylan Hatt , Taylor J. Hoyt , In Sung Jang , Rachael L. Beaton , Christopher R. Burns , Myung Gyoon Lee , Andrew J. Monson , Jillian R. Neeley , M. M. Phillips , Jeffrey A. Rich , and Mark Seibert.The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch[J].The Astrophysical Journal,2019,882(Number 1):34-63.
[6] Siyang Li , Adam G. Riess , Stefano Casertano,Gagandeep S. Anand , Dan Scolnic , Wenlong Yuan , Louise Breuval , and Caroline D. Huang.Reconnaissance with JWST of the J-region Asymptotic Giant Branch in Distance Ladder Galaxies: From Irregular Luminosity Functions to Approximation of the Hubble Constant[J/OL].https://arxiv.org/abs/2401.04777,2024-1-9
[7] Gao, F. search by orcid ; Braatz, J. A. ; Reid, M. J. search by orcid ; Lo, K. Y. ; Condon, J. J. ; Henkel, C. ; Kuo, C. Y. ; Impellizzeri, C. M. V. ; Pesce, D. W. search by orcid ; Zhao, W. The Megamaser Cosmology Project. VIII. A Geometric Distance to NGC 5765b [J].The Astrophysical Journal,2016,817(Number2):17-65
[8]王焘.用引力波测定哈勃常数[J].物理教学,2018,40(02):2-4+19.
[9]胡建萍,余海,王发印.哈勃常数危机[J].科学观察,2023,18(06):21-23.DOI:10.15978/j.cnki.1673-5668.202306004
[10] 蔡荣根,李理,王少江.哈勃常数危机[J].物理学报,2023,72(23):277-293.
[11] Scolnic, D. M. ; Jones, D. O. search by orcid ; Rest, A. ; Pan, Y. C. ; Chornock, R. search by orcid ; Foley, R. J. ; Huber, M. E. ; Kessler, R. search by orcid ; Narayan, G. search by orcid ; Riess, A. G. ; Rodney, S. search by orcid ; Berger, E. search by orcid ; Brout, D. J. ; Challis, P. J. ; Drout, M. ; Finkbeiner, D. search by orcid ; Lunnan, R. search by orcid ; Kirshner, R. P. ; Sanders, N. E. ; Schlafly, E. search by orcid ; Smartt, S. search by orcid ; Stubbs, C. W. search by orcid ; Tonry, J. search by orcid ; Wood-Vasey, W. M. search by orcid ; Foley, M. search by orcid ; Hand, J. ; Johnson, E. ; Burgett, W. S. search by orcid ; Chambers, K. C. search by orcid ; Draper, P. W. search by orcid ; Hodapp, K. W. search by orcid ; Kaiser, N. search by orcid ; Kudritzki, R. P. ; Magnier, E. A. search by orcid ; Metcalfe, N. search by orcid ; Bresolin, F. search by orcid ; Gall, E. ; Kotak, R. search by orcid ; McCrum, M. ; Smith, K. W.The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample[J].The Astrophysical Journal,2018,859(Number2):101-128
[12] Dan Scolnic , Dillon Brout, , Anthony Carr , Adam G. Riess, , Tamara M. Davis , Arianna Dwomoh , David O. Jones , Noor Ali , Pranav Charvu , Rebecca Chen , Erik R. Peterson , Brodie Popovic , Benjamin M. Rose , Charlotte M. Wood , Peter J. Brown, , Ken Chambers, David A. Coulter , Kyle G. Dettman , Georgios Dimitriadis , Alexei V. Filippenko, , Ryan J. Foley , Saurabh W. Jha , Charles D. Kilpatrick , Robert P. Kirshner, , Yen-Chen Pan , Armin Rest , Cesar Rojas-Bravo , Matthew R. Siebert , Benjamin E. Stahl , and WeiKang Zheng.The Pantheon+ Analysis: The Full Data Set and Light-curve Release[J].The Astrophysical Journal,2022,938(Number2):113-127
[13] 杨英杰.哈勃常数,宇宙曲率及加速膨胀的研究[D].华中科技大学:华中科技大学, 2020.
[14] 赵君亮.造父变星周光关系之实测研究进展[J].天文学进展,2013,31(03):287-306.
[15] Mauricio Cruz Reyes, Richard I. Anderson.A 0.9% Calibration of the Galactic Cepheid luminosity scale based on Gaia DR3 data of open clusters and Cepheids[J/OL].https://arxiv.org/abs/2208.09403,2022-8-19
| name | zcmb | zhel | dz | mb | dmb |
| 03D1au | 0.50309 | 0.50309 | 0 | 22.93445 | 0.12605 |
| 03D1aw | 0.58073 | 0.58073 | 0 | 23.52355 | 0.1372 |
| 03D1ax | 0.4948 | 0.4948 | 0 | 22.8802 | 0.11765 |
| 03D1bp | 0.34593 | 0.34593 | 0 | 22.11525 | 0.111 |
| 03D1co | 0.67767 | 0.67767 | 0 | 24.0377 | 0.2056 |
| 03D1ew | 0.8665 | 0.8665 | 0 | 24.34685 | 0.17385 |
| 03D1fc | 0.33094 | 0.33094 | 0 | 21.7829 | 0.10685 |
| 03D1fq | 0.79857 | 0.79857 | 0 | 24.3605 | 0.17435 |
| 03D3aw | 0.44956 | 0.44956 | 0 | 22.78895 | 0.14135 |
| 03D3ay | 0.37144 | 0.37144 | 0 | 22.28785 | 0.1245 |