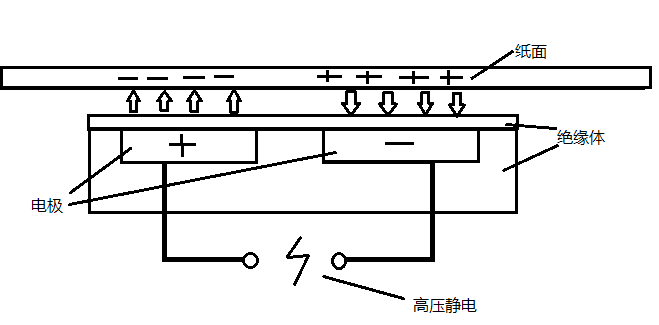
图1
练习书法、绘画既能丰富业余生活,又能修身养性,陶冶情操,是一项得到众人青睐的艺术活动。但是,在进行这项活动时,人们经常面临一个困扰,那就是,一旦有风,纸容易被吹起来;风稍微大点的话,使用镇纸也无济于事。

图1
最近,我在物理课程中学习了静电吸附的原理,产生了一个奇妙的想法:是否可利用静电的吸附性代替镇纸呢?在得到老师和家长的鼓励后,我通过阅读大量相关文献,反复进行试验,设计出了一个静电书画台,可以令人满意地解决“纸欲静而风不止”的问题。
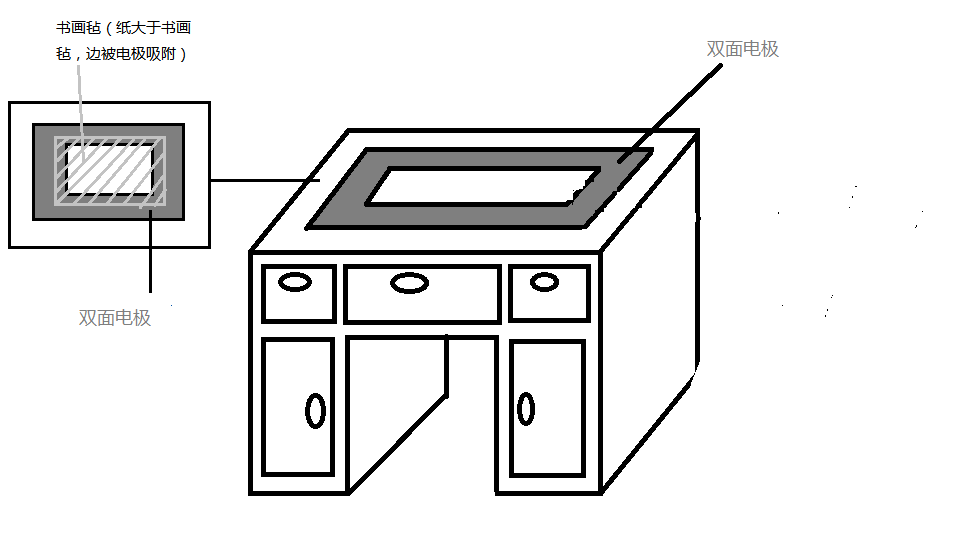
图2
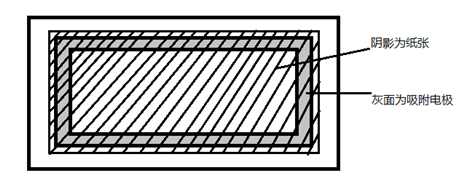
图3
本设计中采用直流型电源获得双极型静电吸附电,主要考虑直流流型电源下产生的垂直吸附力相对大
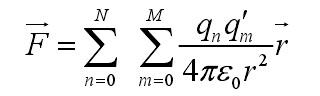
图4
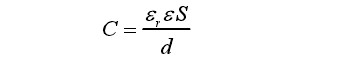
图5
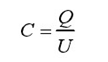
图6
在练习书画时,先将纸张平铺在电极板上面,铺好后接通交流电。也可以先接通交流电,再将纸铺上去。
静电书画台之所以能得到这样的奇妙效果,主要是由于静电吸附的作用,具体而言,静电吸附电极所产生的吸附力实际上就是电场作用力,而电场作用力均服从于库伦定律,现假设已知电极和纸面上的电荷分布情况,则由库伦定律,纸面与电极间的吸附力可表示为:
(1-1)
qn:表示极板上的点电荷
qm:表示纸面上的点电荷
r: 为两点电荷间距离
纸面与吸附电极间的吸附力实质为纸面上电荷与吸附电极上电荷间的库伦力的矢量和。吸附力与电荷间距离的平方成反比,与电荷量成正比。当吸附电极与纸面的距离不变时,通电压更高的静电或增大电极面积,可使电极对纸面的吸附力增加。
从静电吸附电极工作原理的分析中,可以看到,纸面与吸附电极共同构成了电容系统。尽管这里讨论的是共面双面电极型静电吸附电极和纸面所构成的同面散射场电容,但通过平行板电容器的计算式:
(1-2)
依然可定性地知道,电容的大小与纸面和绝缘层的相对介电常数,以及吸附电极的几何尺寸有关。而根据电容的定义式:
(1-3)
可以看出,一方面,一定电压下,电容的大小影响着电容所能够存储的电量。另一方面,对于电容固定的系统,提高吸附电极的两极间电压,也可以提高吸附电极上的电量,从而间接提高吸附力。但是,电压并非可以无限加大,这是由于任何材料都有自身的介电强度极限,一旦超过,材料就会发生击穿,导致吸附失效,并致使吸附设备及纸面损坏。此外,单方面提高电压,加大了对高压静电发生器的负荷,在工程上增加了不必要的难度。
综上所述,影响静电吸附电极吸附力的主要因素有以下四点:
(1)电源电压,对于特定的静电吸附电极和纸面,加载电压直接影响吸附电极上的荷电大小,从而影响吸附力大小。
(2)绝缘层参数,根据公式
(1-4)
绝缘层厚度直接影响电极与纸面间的距离,从而影响吸附力大小。而绝缘层作为吸附电容的介质层的一部分,其厚度和相对介电常数对吸附电容均有影响。
(3)纸面特征及材质,纸面的粗糙程度,决定了电极与纸面间的空气层厚度,此外,纸面作为吸附电容的介质层的一部分,其相对介电常数同样对吸附电容的大小起影响。
(4)共面双面电极型是双极型静电吸附电极的基本形式,通过分析其简化模型的吸附力与加载电压间的关系,可以进一步得到其他双极型静电吸附电极吸附力与加载电压间的关系。共面双面电极型静电吸附电极的简化模型如下图所示。
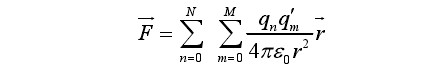
图7
共面电极面积为S,长、宽、厚分别为 w,l,d1。极间间距为 dj。为防止击穿,电极间填充了相对介电常数为 εr1的绝缘材料。绝缘层的相对介电常数为 εr2,厚度为 d2,空气层厚度为 d0。纸面认为介电常数为 εr3。两面电极相距距离足够远,间距 dj远大于面电极的宽度 w,忽略两面电极上电荷间的相互作用,则可认为面电极上的电荷均匀分布,同时,由于绝缘层、空气层的厚度远小于面电极的长 l 和宽 w,忽略边缘效应。因此可以认为面电极与纸面之间的电场为均匀场。由于正负电极存在对称关系,因此正负电极上的吸附力应大小相等所以,模型只需分析正面电极的吸附力即可。如前一节关于静电吸附电极的基本原理分析所述,吸附电极与纸面之间构成电容系统。
纸面内的总电场强度 E,由正极板上的正电荷所产生的电场 E0和由纸面表面极化产生的束缚电荷所产生的退极化场 E′叠加而成,如下式所示:
(2-1)
由于纸面束缚电荷及正极板上电荷均匀分布,E0、E′可利用高斯定理计算如下:
(2-2)
(2-3)
将式(2-2)及式(2-3)代入式(2-1)可得:
(2-4)
根据静电场边界条件,极板上的电荷分布于极板表面。设极板靠近纸面一端的电荷面密度为 σ2,远离纸面一端的电荷面密度为 σ1,则有:
(2-5)
另一方面,金属极板内的电场可表示为左边表面电荷所产生的场强E2、右边表面的场强 E1以及纸面上束缚电荷的场强 E3三者的叠加,如图所示。由于静电屏蔽作用,金属内部合场强为零,因此有:
(2-6)
利用高斯定理,(2-6)式可进一步改写为:
(2-8)
由式(2-8)可以看出,由于纸面表面束缚电荷的作用,导致金属纸面左表面和右表面上的分布的电荷不等。
联立式(2-5)、式(2-8)及式(2-4)可得:
(2-9)
(2-10)
又由于极化率与相对介电常数存在如下关系:
(2-11)
将上式代入式(2-4)、式(2-9)及式(2-10)
(2-12)
(2-13)
(2-14)
由于电极表面电荷均匀分布,且空气层间的电场也是均匀分布,空气层中的电位移量可由高斯定理计算得:
(2-15)
空气层电场强度计算如下:
(2-16)
静电吸附电极单位面积的吸附力可表达有该点的电场能量密度,则:
(2-17)
,得到正极板上电量与单位面积吸附力间的关系:
(2-18)
,可得到单位面积吸附力与加载电压间的关系:
(2-19)
对于给定的静电吸附电极和纸面,上式(2-19)中,电容 Cx、S 以及εr3属于吸附系统的结构参数,是常量。因此,由上式(2-19)可知,在库伦力作用下,电荷均匀分布的电极板,单位面积的吸附力与加载电压平方成正比。从上式中还可以看到,纸面的相对介电常数εr3对吸附力的影响。由式(2-19)可知,纸面的相对介电常数越大,吸附力也将越大。当纸面的相对介电常数 εr3趋于无穷大时,纸面变成金属,吸附电极退化为平行板电容,此时,由(2-18)式可知,吸附电极电量不变的情况下,金属对纸面所产生的吸附力最大。此外,如上文所述,纸面的相对介电常数将会影响吸附电容 Cx的大小。
实际上,当考虑共面双面电极上由于两电极间的相互作用而导致的电荷分布不均的情况时,可以将电极划分成足够小的面积,以至于该面元上面的电荷仍然可以看作是均匀分布,则上式(2-19)可改写为:
(2-20)
上式中,dCx和 dS 都是关于电极面元的变量。由于极板为等势体,Ua在对电极面积求积分时可以提到积分号外,有:
(2-21)
所以,即使是在电荷非均匀分布的共面双面电极型静电吸附电极上,库伦作用下电极吸附力 F 与加载电压Ua的平方成正比的关系仍然成立。
5.1 实验材料
(1)梳状电极(自制)
(2)共面双面电极(自制)
(3)交流与直流高压发生器模块(通入3v电压变到7kv)
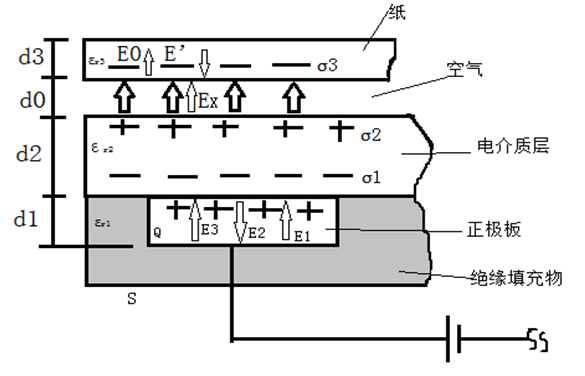
图8
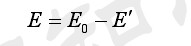
图9
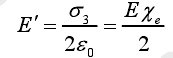
图10
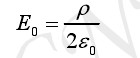
图11
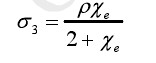
图12
5.2 实验内容和讨论
(1)绝缘体与吸附力的关系
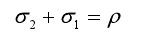
图13
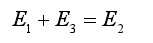
图14
没贴透明胶之前给高压发生模块通1.5v,便产生了电火花,空气介质被击穿。贴了透明胶以后,给高压发生模块通的最高电压可到2.2v,电极构成的电容内电压变大,所以电场随之变大,根据库仑定理,吸附力变大。
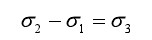
图1
不透明胶换成了绝缘胶带后,高压发生模块通的最高电压可到3v,电极构成的电容系统内所存电压更大,所以吸附力也更大
实验总结:在梳妆电极表面贴上介电系数较高的绝缘体,可使在梳状电极两端通上较高的电压,并且提高吸附力。
(2)梳状电极与双面电极的比较
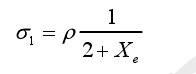
图1
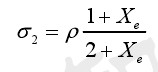
图1
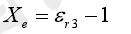
图1
究其原因,吸附力的切向与垂直吸附力与电极的结构有关。梳状电极的正负电压交错,垂直方向的电场有一些平衡掉了,垂直方向的电场就小,所以库仑力就小,所以梳状电极的垂直吸附力弱。而双面电极一整个面只有单种电压并且分布均匀所以就没有这个问题,它的电场与梳妆电极相比就较大,所以双面电极的垂直吸附力强。
梳状电极在水平方向正负两者相吸,所以切向吸附力较大,切向的电场较大,库仑力就较大,所以梳妆电极的切向吸附力较大;而双面电极一个面上只有一种电荷并且分布均匀,对切向吸附力没有增强,不会像梳妆电极那么大,所以双面电极的切向吸附力较弱。
结论:双面电极的垂直吸附力因其结构关系而最大,静电书法台主要利用静电的垂直吸附力,因此共面双面电极作为产生静电的电极是更加理想的方案。
(3)关于电荷弛豫现象造成荷电现象
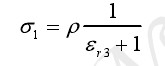
图1
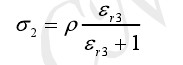
图1
发现这个现象后,我想如果能找到一个能够很好地延长延长荷电现象的时间的介电物质,就有可能在断电后使电极仍长时间具有吸附力,这将大大减少电能的消耗,同时也减少了触电的可能性。
结论:目前我所找到的材料都无法产生长时间的荷电现象,荷电现象现象会对材料产生损害,使电极的弛豫时间不断减少,目前我还未发现损耗较小的电极,所以这个方面还有待我以后的研究。
(4)关于静电吸附对水和颜料的影响
众所周知,静电会对水产生吸附,所以所以在研究中我针对这个现象作了一定的实验。
经过实验,我发现梳状电极会对水有明显的影响,当水在梳妆电极上时,电极上的梳状结构会对水产生吸附,使水产生不规则变化,对作画产生影响。
而水在双面电极上时,因为双面电极的吸附力十分均匀,没有像梳状电极两个极板正负极之间吸附力,所以水未产生明显的不规则变化,经过实际中的实验,它不会影响作画。
至此,静电书画台可以作为书画爱好者的好帮手,风欲吹而纸能静,可以让书画爱好者沉浸于艺术创作而无惧于风的干扰。
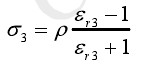
图21
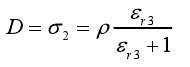
图22
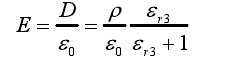
图23
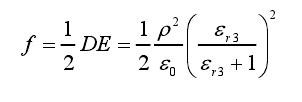
图24
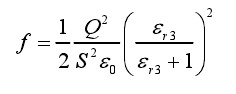
图25
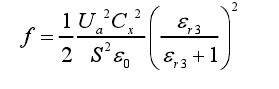
图26
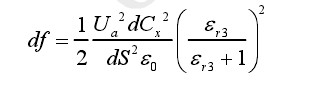
图27
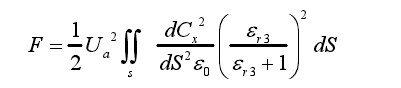
图28

图29

图30

图31

图32

图33

图34

图35

图36

图37